| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- OOP
- 운영체제
- DFS
- stack
- 코딩 테스트
- queue
- 프로세스
- springboot
- 다익스트라
- Python
- 객체지향 프로그래밍
- error
- 스택
- java
- integretion test
- OS
- 파이썬
- 큐
- SW Expert Academy
- DP
- 캡슐화
- 데드락
- 백준 #
- 백준
- 자료구조
- 유니크 키
- unionfind
- BFS
- 디바이스 입출력
- 논리 메모리
- Today
- Total
middlefitting
[OS] 사용자 프로그램 물리 메모리 할당, 연속할당과 불연속 할당에 관하여 본문
물리 메모리 영역
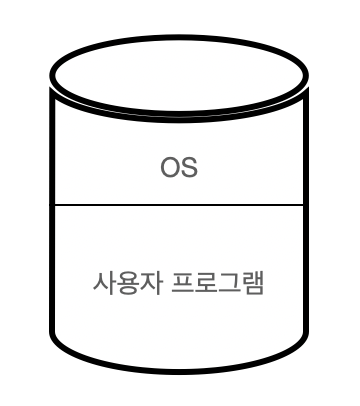
물리 메모리 영역은 일반적으로 OS 상주역역, 사용자 프로세스 영역으로 나뉘어 사용됩니다.
OS 상주역역은 주로 낮은 주소 영역을 사용하고, 사용자 프로세스 영역은 높은 영역을 사용하는데,
사용자 프로세스 영역의 할당 기법에는 연속 할당, 불연속 할당 기법이 존재합니다.
여기서 운영체제의 메모리 할당은 고려하지 않아도 되는 것일까요?
운영체제는 컴퓨터가 시작하고 종료될때까지 가장 먼저 실행되고 멈추지 않고 돌아가는 프로그램입니다.
따라서 운영체제는 당연히 물리 메모리에 올라가 있다고 생각하시면 될 것 같습니다.
연속 할당
연속 할당이란 프로그램이 통째로 메모리 한 장소에 올라가는 것을 말합니다.
통째로 올라간다는 것은 메모리의 연속적인 공간에 적재된다는 것을 말합니다.
연속할당의 방법에는 고정분할과 가변분할 방식이 존재합니다.
고정분할 방식
고정 분할 방식은 물리적 메모리를 몇 개의 영구적 분할(파티션)로 나누는 것을 말합니다.
파티션 크기는 자유롭게 나누게 되지만, 프로그램은 파티션 사이즈가 프로그램 이상인 최초의 빈 파티션을 찾아 들어가게 됩니다.
고정 분할 방식은 필연적으로 외부조각과 내부조각이 발생하게 됩니다.
외부조각이란 조각이 작아서 프로그램을 넣지 못하고 놀고 있는 메모리 공간을 말하고,
내부 조각이란, 프로그램에게 할당을 해주었지만 공간이 남아서 놀게 되는 공간을 말합니다.
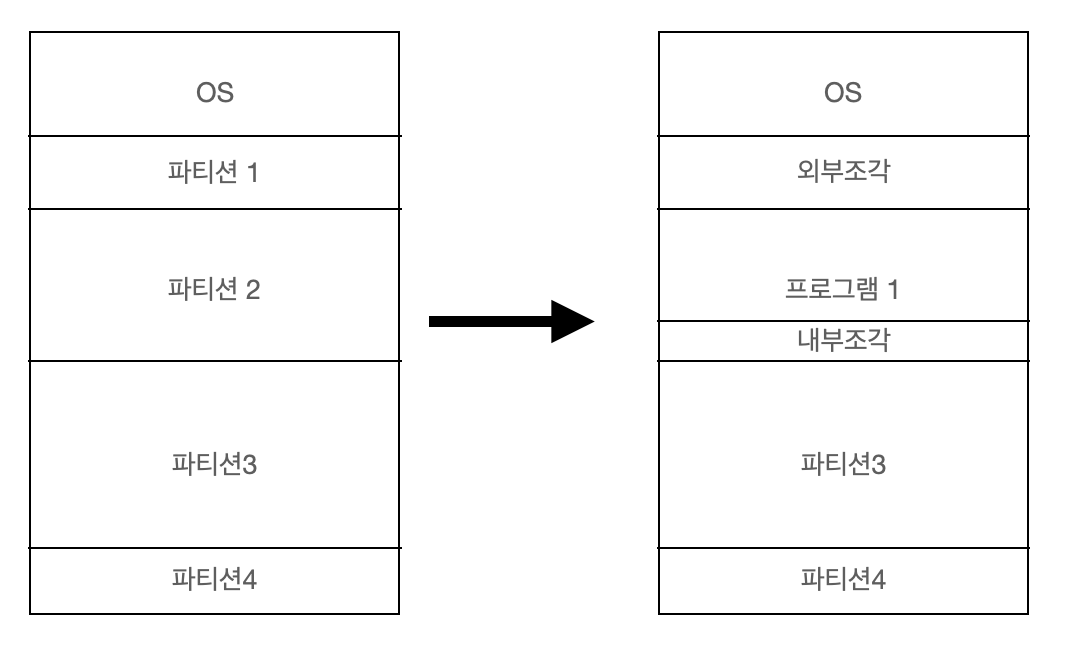
간단한 그림으로 보여드리자면 이런 느낌입니다.
왼쪽의 파티션에게 그림처럼 파티션이 존재할 때, 프로그램1을 메모리에 올려야 하는 상황입니다.
프로그램1은 파티션1보다 사이즈가 크기 때문에 그 다음 파티션인 파티션2에 들어가게 되었습니다.
파티션1은 현재 상태에서 조각이 작아 프로그램을 할당해 주지 못했으니 외부조각으로 볼 수 있고,
파티션2가 프로그램1을 올려주고 공간이 남게 되어서 해당 부분은 내부조각이 된 것입니다.
가변 분할 방식
가변분할 방식은 고정분할방식과 다르게 메모리 영역을 미리 나누어 놓지 않는 것을 말합니다.
메모리에 차곡차곡 프로그램을 올리는 방식인데, 파티션을 나누어 놓지 않으니 내부조각은 발생하지 않을 것입니다.
하지만 중간에 프로그램이 종료되어 중간에 빈 공간이 발생하였을때, 새로 올릴 프로그램이 해당 영역보다 사이즈가 커서 메모리에 올리지
못하는 상황은 발생할 것이기 때문에, 외부 조각은 발생하게 됩니다.
그렇다면 외부 조각을 해결할 수 있는 방법은 없는 것일까요.
compaction 이라는 방법이 존재하기는 합니다.
해당 방법은 외부 조각 문제를 해결하기 위해 사용중인 메모리 영역을 한 장소로 모아서,
hole들을 모아 큰 block을 만드는 방법을 말합니다.
좋아 보이는 방법이지만 프로그램을 이동시키는 것은 비용이 많이 발생한다는 점을 고려하여 적용하여야 할 것입니다.
작은 이동을 통해 큰 hole을 만드는게 효율적일 수도 있으니 상황에 따라 유연한 동작도 필요할 것입니다.
더불어 해당 기법을 사용하기 위해서는 프로세스의 주소가 동적으로 재배치가 가능해야 하므로 최소 런타임 바인딩을 사용하여야 합니다.
가변분할 방식에서운영체제는 메모리의 어느 부분이 사용되고 어느 부분이 현재 외부 조각인지 등 이러한 정보에 대해 알고있어야 합니다.
즉 프로그램이 실행될 때 어떠한 조각에 프로그램을 올려서 조각을 최소화하고 시간을 최소화할 것인지도 중요합니다.
First-fit
가장 발견되는 빈 메모리 공간에 프로그램을 넣는 방식을 말합니다.
빈 공간(hole)을 찾는 오버헤드가 작다는 장점이 존재합니다.
Best-fit
hole을 다 뒤져보고 크기가 프로그램에 가장 근사한 크기에 할당하는 것을 말합니다.
hole을 찾는 오버헤드는 존재하지만 조각의 발생을 최소화할 수 있는 방법입니다.
Worst-fit
hole의 크기가 가장 큰 곳에 프로그램을 올리는 방법입니다.
가장 큰 hole을 찾는 오버헤드, 가장 큰 외부 조각을 생성하는 방법이기 때문에,
First-fit과 Best-fit에 비해 효율적인 방법이라고 할 수 없는 방법입니다.
불연속 할당
불연속 할당은 프로그램이 메모리의 여러 영역에 분산되어 올라갈 수 있는 것을 말합니다.
현대 시스템에서는 당연히 불연속 할당 기법을 사용하며, 보통 페이지 단위로 메모리가 올라가고 내려갑니다.
대표적인 방법에는 페이징 기법, 세그먼테이션 기법, 페이지 세그먼테이션기법이 존재합니다.
Paging
페이징 기법은 프로세스의 가상 메모리를 동일한 사이즈의 페이지 단위로 나누어서, 가상 메모리 내용을 페이지 단위로 불연속하게
저장하는 것을 말합니다. 보통 논리 메모리가 물리 메모리보다 크기 때문에, 모든 페이지가 물리 메모리에 올라간다는 것은 보장할 수 없고
일부는 물리 메모리에, 일부는 backing storage(swap)에 저장될 것입니다.
물리 메모리에는 페이지와 동일한 크기에 페이지 프레임이 존재하게 되는데, 해당 페이지 프레임에 들어가는 방식이기 때문에 외부조각은
발생하지 않게 되고, 프로세스의 크기가 꼭 페이지의 배수로 나누어 떨어지지는 않으니 내부 조각은 아주 약간 발생할 수 있을 것입니다.
또한 해당 페이지 정보는 페이지 테이블에 존재하여 논리 메모리에 저장된 페이지가 어느 페이지 프레임에 존재하는지 확인할 수 있습니다.
Segmentation
세그먼테이션 기법은 프로그램을 의미 단위인 여러 개의 세그먼트로 구성하는 것을 말합니다.
즉 세그먼트마다 별도의 크기를 가져서, 해당 의미단위마다 메모리에 저장하는 것을 말합니다.
의미 단위로는 code, data, stack은 물론이고, main 등 함수들도 의미단위로 사용할 수 있습니다.
세그먼테이션 방식도 페이징과 비슷하게 세그먼트 정보를 저장하는 세그먼트 테이블이 프로그램별로 존재하게 됩니다.
페이징 방식과 비교해서는 장단점이 존재하는데요,
장점으로는 의미 단위로 쪼개놓았기 때문에, Protection에 있어 권한 부여 및 공유가 자연스럽다는 점입니다. 페이징 방식 방식에서는
code, data, stack도 각각 다른 페이지 프레임에 쪼개져 들어가기 때문에 권한 작업이 어려워지게 됩니다.
단점으로는 세그먼트 크기가 균일하지 않기 때문에 중간중간 외부조각들이 발생하게 된다는 점이 되겠습니다.
Page Segmentation
페이지 세그먼테이션 방식은 이름처럼 페이징 방식과 세그먼테이션 방식을 혼합해서 사용하는 것이라고 생각하시면 됩니다/
즉 세그먼트 하나가 여러개의 페이지로 구성되는 방식입니다.
의미나 보안 면에서는 세그먼트 방식의 장점을 챙길 수 있고,
메모리 면에서는 실제 저장은 페이지로 쪼개서 저장하므로 외부 조각의 발생을 막을 수 있습니다.
즉 두가지 방식의 장점을 모두 사용할 수 있는 방식이 되겠습니다.
출처
KOWS 운영체제 - 반효경 교수님 - Memory Management 2, 3, 4
'OS' 카테고리의 다른 글
| 프로그램은 어떻게 프로세스가 될까 (1) | 2023.10.28 |
|---|---|
| [OS] 가상 메모리(Virtual Memory)에 관하여 (0) | 2023.02.06 |
| [OS] 논리(Logical) 메모리와 물리(Physical) 메모리에 관하여 (0) | 2023.02.04 |
| 데드락(Deadlock)을 방지하는 방법에 관하여 (0) | 2023.02.02 |
| 데드락(Deadlock) 이란 무엇인가. (0) | 2023.02.01 |

